【แถบ Bollinger①】เกี่ยวกับส่วนเบี่ยงเบนมาตรฐาน

ปัญหาเกี่ยวกับส่วนเบี่ยงเบนมาตรฐาน

「ใน Bollinger Bands มีคำอธิบายว่า ความน่าจะเป็นที่ราคาจะอยู่ภายในช่วง -2σ ถึง +2σ ตามสถิติคือ 95.5% แต่เรื่องนี้เป็นความผิดพลาด จงอธิบายอย่างย่อ」

คุณจอห์น บอลลินเจอร์ ผู้พัฒนาชุด Bollinger Band ได้ระบุในหนังสือว่า「แม้ราคาจะพ้นขอบบน(+2σ) ก็ไม่ได้หมายความว่าเป็นสัญญาณขาย และแม้จะทะลุตอบล่าง(-2σ) ก็ไม่ได้หมายความว่าเป็นสัญญาณซื้อ」อย่างชัดเจน

แต่ถึงอย่างนั้น สัญญาณการซื้อขายที่ผิดพลาดยังแพร่หลายอยู่ในญี่ปุ่น ทั้งที่ผู้สร้างดัชนีปฏิเสธมันแล้ว

แน่นอนว่าเป็นเพราะไม่เข้าใจนิยามและสูตรการคำนวณของอินดิเคเตอร์ทางเทคนิคอย่างถูกต้อง

คำตอบ

「การเคลื่อนไหวของราคายังไม่เป็นการกระจายปกติ」

บทอธิบาย

ก่อนอธิบาย Bollinger Band เราจะอธิบายเกี่ยวกับส่วนเบี่ยงเบนมาตรฐาน

ถ้าไม่เข้าใจส่วนเบี่ยงเบนมาตรฐาน จะไม่สามารถเข้าใจ Bollinger Band ได้อย่างถูกต้อง

ส่วนเบี่ยงเบนมาตรฐานคือค่าที่แสดงระดับการกระจายของข้อมูล

ตัวอย่างคิดจากคะแนนสอบ

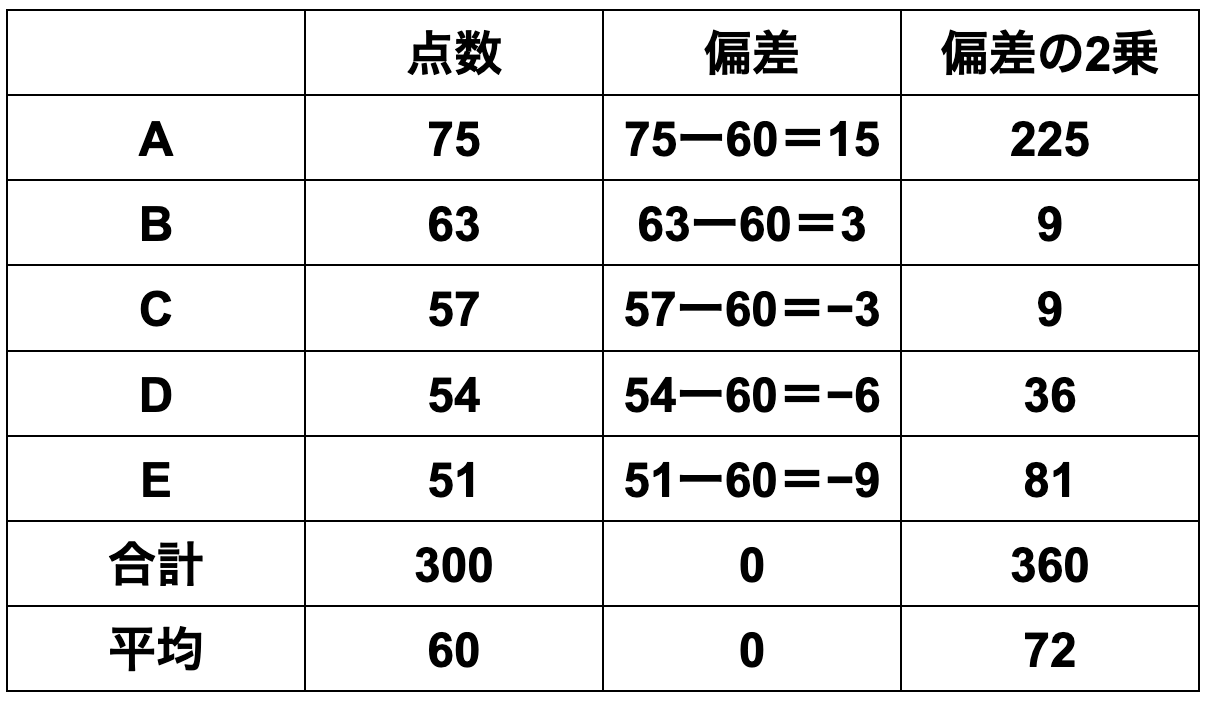
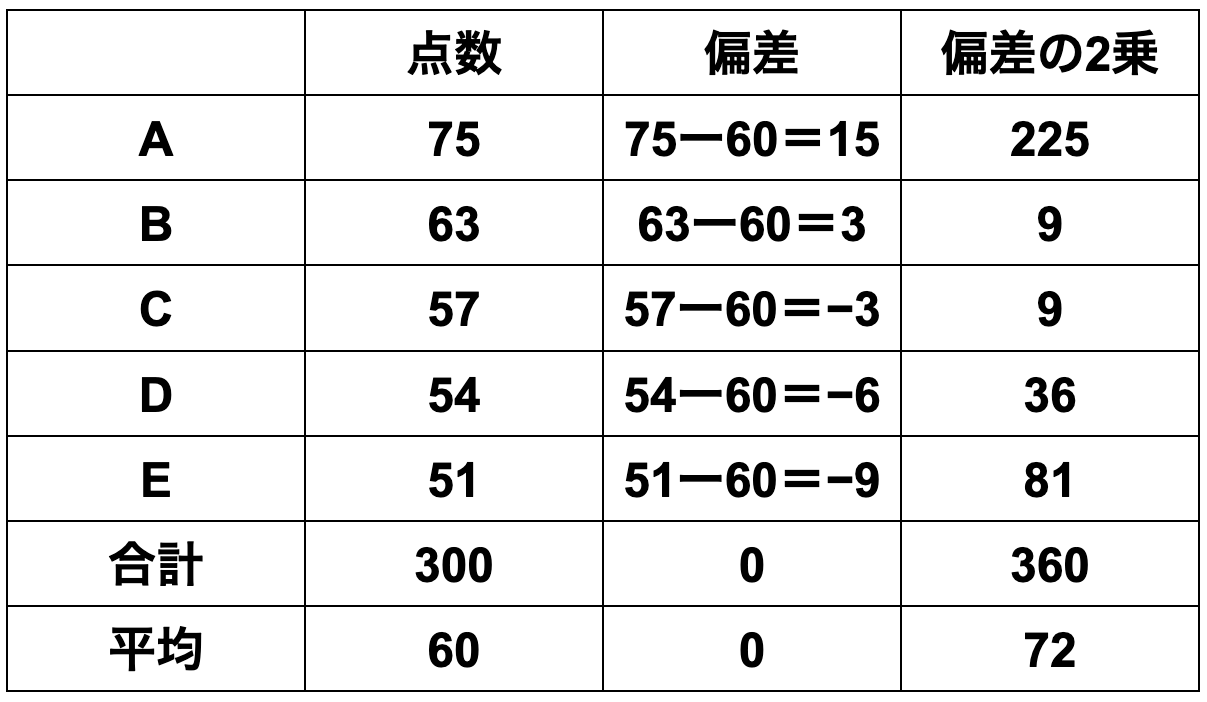
คะแนนของกลุ่มคน 5 คนดังนี้

กลุ่มที่ 1 [75 คะแนน, 63 คะแนน, 57 คะแนน, 54 คะแนน, 51 คะแนน]

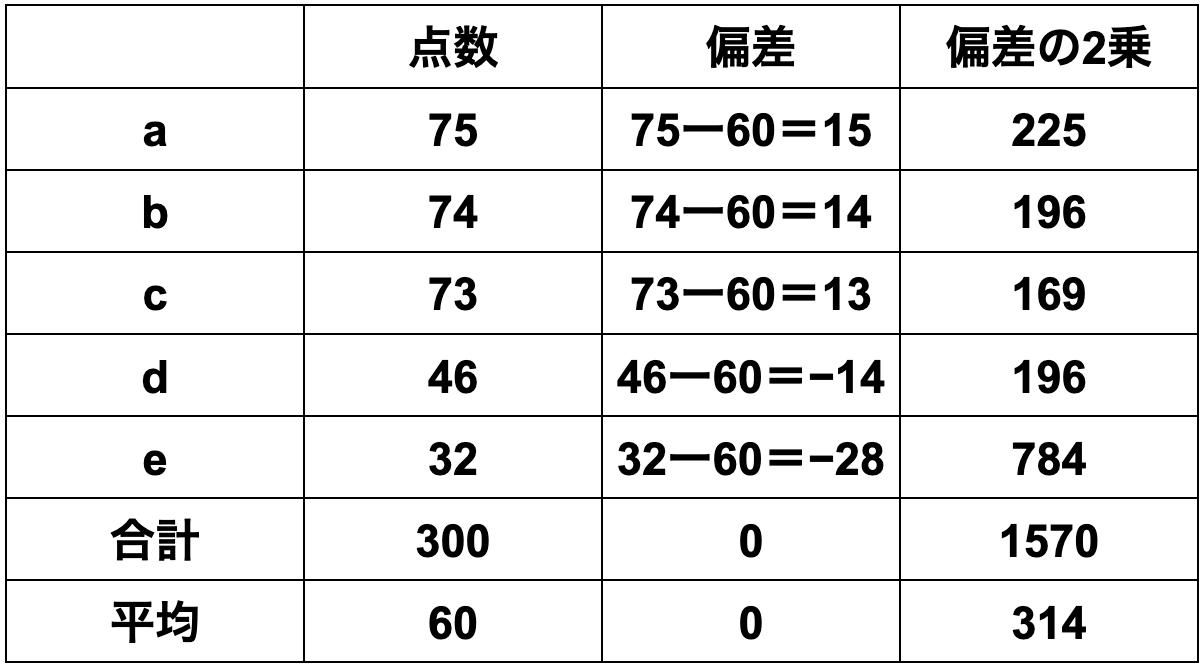
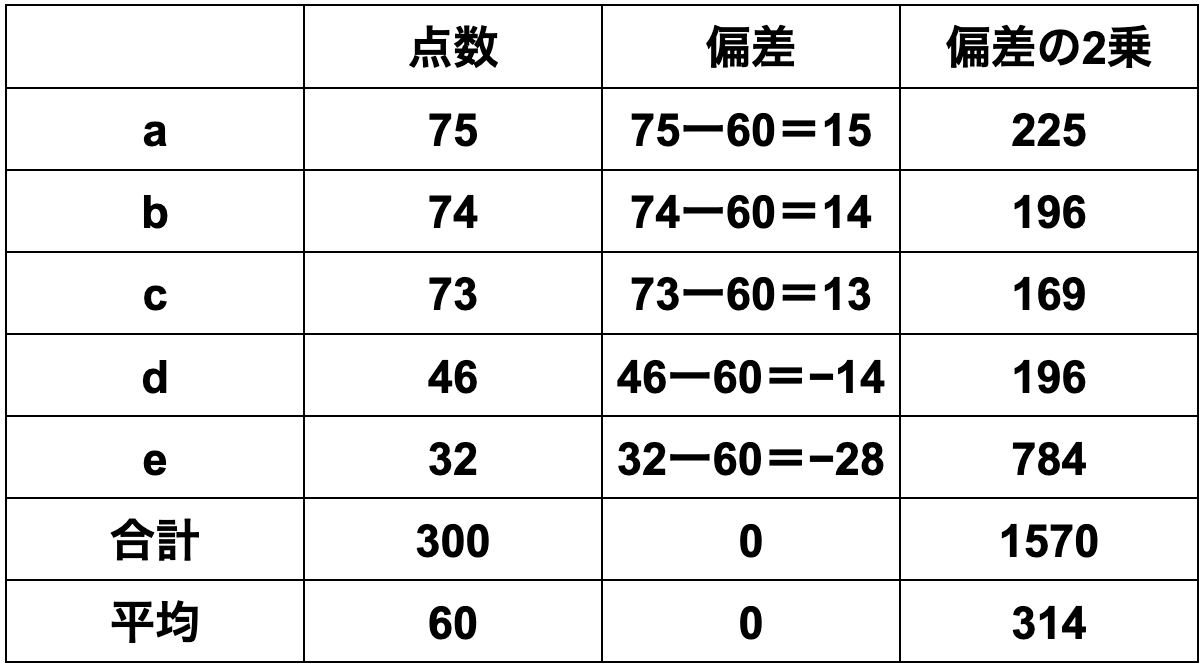
กลุ่มที่ 2 [75 คะแนน, 74 คะแนน, 73 คะแนน, 46 คะแนน, 32 คะแนน]

ดังนั้น

กลุ่มที่ 1 จึง

① ค่าเฉลี่ย = ผลรวมข้อมูล ÷ จำนวนข้อมูล

=(75+63+57+54+51)÷5

=60

② ส่วนเบี่ยงเบน = ค่าข้อมูลแต่ละตัว − ค่าเฉลี่ย

＝[15、3、-3、-6、-9]

③ ความแปรปรวน = ผลรวมของกำลังสองของส่วนเบี่ยงเบน ÷ จำนวนข้อมูล

＝(225+9+9+36+81)÷5

＝72

④ ส่วนเบี่ยงเบนมาตรฐาน = √72 = 8.48

กลุ่มที่ 2

① ค่าเฉลี่ย = ผลรวมข้อมูล ÷ จำนวนข้อมูล

=(75+74+73+46+32)÷5

=60

② ส่วนเบี่ยงเบน = ค่าข้อมูลแต่ละตัว − ค่าเฉลี่ย

＝[15、14、13、-14、-28]

③ ความแปรปรวน = ผลรวมของกำลังสองของส่วนเบี่ยงเบน ÷ จำนวนข้อมูล

＝(225+196+169+196+784)÷5

＝314

④ ส่วนเบี่ยงเบนมาตรฐาน = √314 = 17.72

กลุ่มที่ 2 มีส่วนเบี่ยงเบนมาตรฐานมากกว่า จึงเห็นการกระจายที่มากกว่า

นิยามของ “ค่าเฉลี่ยแนวตั้ง” ที่ใช้ในการสอบเข้ามหาวิทยาลัยคือ

ค่าเฉลี่ยแนวแนวแกน = 50 + (คะแนน − คะแนนเฉลี่ย) ÷ ส่วนเบี่ยงเบนมาตรฐาน × 10

ในกรณีการสอบนี้

กลุ่มที่ 1 ของอาさん, กลุ่มที่ 2 ของอาさん ต่างมีคะแนนเฉลี่ย 60 คะแนนและได้ 75 คะแนน แต่ค่าเฉลี่ยแนวทางต่างกัน

偏差値ของกลุ่มที่ 1 อาさん

＝50+(75−60)÷8.48×10

=67.7

偏差値ของกลุ่มที่ 2 อาさん

＝50+(75−60)÷17.72×10

=58.5

อาさんกลุ่มที่ 1 มี偏差値สูงกว่า

ขึ้นอยู่กับการกระจายของข้อมูล ค่าคะแนนที่เท่ากันอาจมีตำแหน่งที่แตกต่างกัน

หากเราคิดเรื่อง “การตรวจสอบการกระจาย” โดยไม่ผ่านการยกกำลังสองและรากที่สอง อาจคิดว่าเห็นความแตกต่างโดยตรงจากค่าเฉลี่ย

แนวคิดนั้นเรียกว่า mean absolute deviation แต่มีข้อบกพร่อง

ยกตัวอย่าง หากมีชั้นเรียน 2 ชั้นที่มีค่าเฉลี่ยคะแนนเท่ากันที่ 50 คะแนน

กลุ่มที่ 1 มี 40 คะแนน 5 คน และ 60 คะแนน 5 คน

กลุ่มที่ 2 มี 0 คะแนน 1 คน, 100 คะแนน 1 คน, 50 คะแนน 8 คน

กลุ่มที่ 2 จะดูมีการกระจายชัดเจนกว่าในทางภาพรวม

อย่างไรก็ตาม ผลรวมของค่าเฉลี่ยแนวต่างจากกันจะเท่ากันคือ 100 คะแนน

เป็นผลให้ mean absolute deviation เท่ากันที่ 10 คะแนน

เพื่อให้วัดความกระจายได้ถูกต้อง จะยกกำลังสองเพื่อทำให้ตัวเลขมีค่ามากขึ้นเมื่อห่างจากค่าเฉลี่ย

เพราะการยกกำลังสองช่วยให้ไม่สนใจทศนิยมบวกหรือลบ

เพื่อกลับสู่หน่วย มีการถอดรากที่สองออก

เมื่อทราบส่วนเบี่ยงเบนมาตรฐานแล้ว เราจะพูดถึงนิยาม Bollinger Band

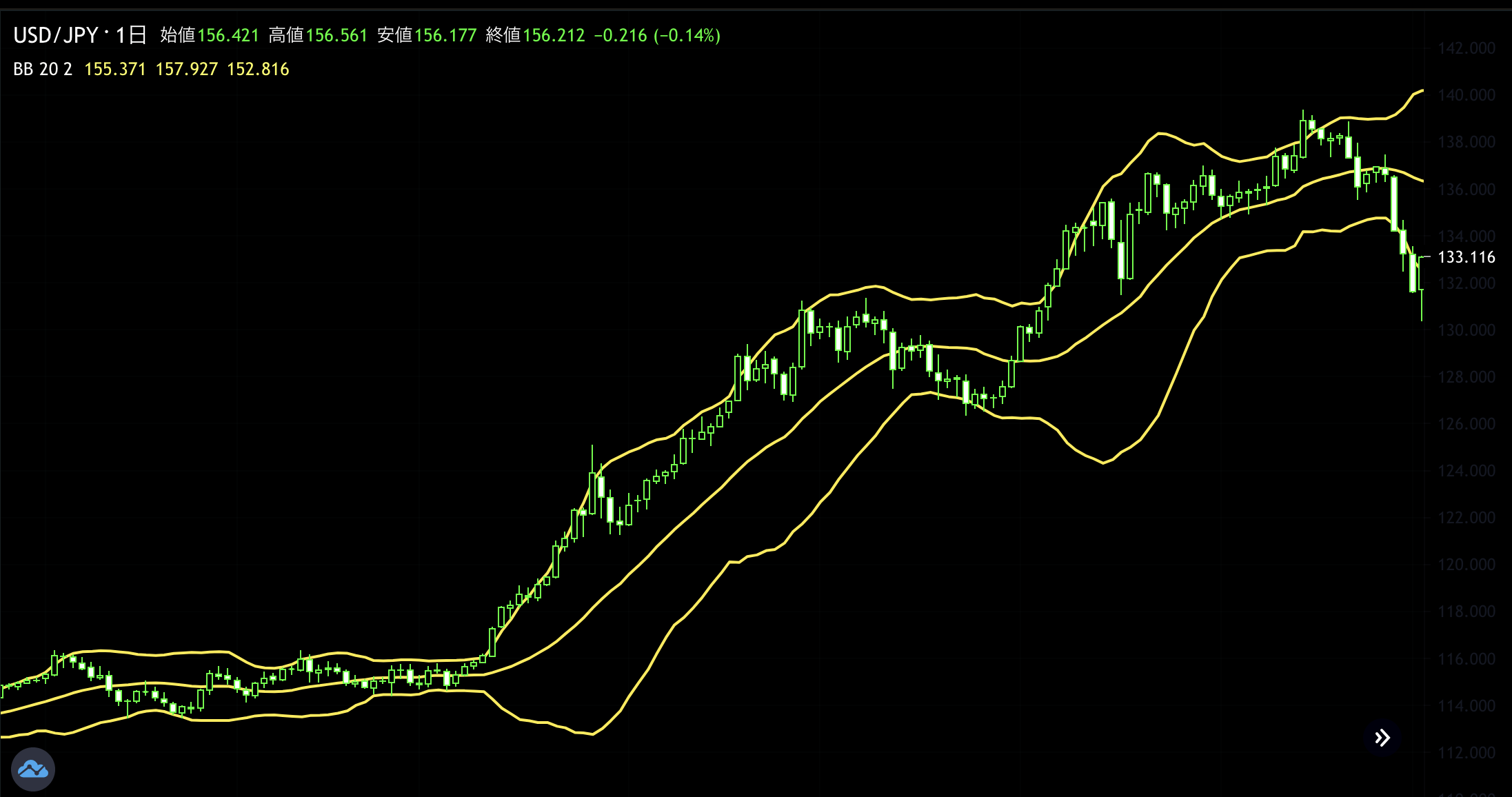
เมื่อคำนวณส่วนเบี่ยงเบนมาตรฐานจากราคาปิด 20 วันที่เป็น σ แล้ว แถบจะจัดวางรอบค่าเฉลี่ยเคลื่อนที่ 20 วันที่เป็นศูนย์กลาง

เส้น +2σ คือส่วนที่บวกราคาของ σ สองเท่า

เส้น −2σ คือส่วนที่ลบ σ สองเท่า

เรียกมันว่า

ดังนั้น Bollinger Band โดยรวมบอกอะไรได้บ้าง? คือ ความผันผวน (volatility)

กลับมาสนทนาเรื่องการสอบ

ส่วนเบี่ยงเบนมาตรฐานของกลุ่มที่ 1 คือ 8.48

ส่วนเบี่ยงเบนมาตรฐานของกลุ่มที่ 2 คือ 17.72

เพราะส่วนเบี่ยงเบนมาตรฐานบ่งบอกการกระจายของข้อมูล ดังนั้น

หมายถึงข้อมูลจะอยู่ในช่วงค่าเฉลี่ยบวก/minus ส่วนเบี่ยงเบนมาตรฐาน

กลุ่มที่ 1 อยู่ที่ 60±8.48 = 51.52–68.48 คะแนน

กลุ่มที่ 2 อยู่ที่ 60±17.72 = 42.28–77.72 คะแนน

เมื่อดูจริง จะพบว่า

ในช่วง ±1 ส่วนเบี่ยงเบนมาตรฐาน

กลุ่มที่ 1 คือ B、C、D

กลุ่มที่ 2 คือ a、b、c、d

หากขยายช่วงออกเป็น ±2 ส่วนเบี่ยงเบนมาตรฐาน

กลุ่มที่ 1 อยู่ที่ 60±8.48×2 = 43.04–76.96 คะแนน

กลุ่มที่ 2 อยู่ที่ 60±17.72×2 = 24.56–95.44 คะแนน

ดังนั้น ทุกคนในทั้งสองกลุ่มจะอยู่ภายในช่วง ±2σ

จากแนวคิดนี้ มีข้ออ้างที่ว่า ช่วงราคาอยู่ใน ±2σ มีความน่าจะเป็น 95.5%

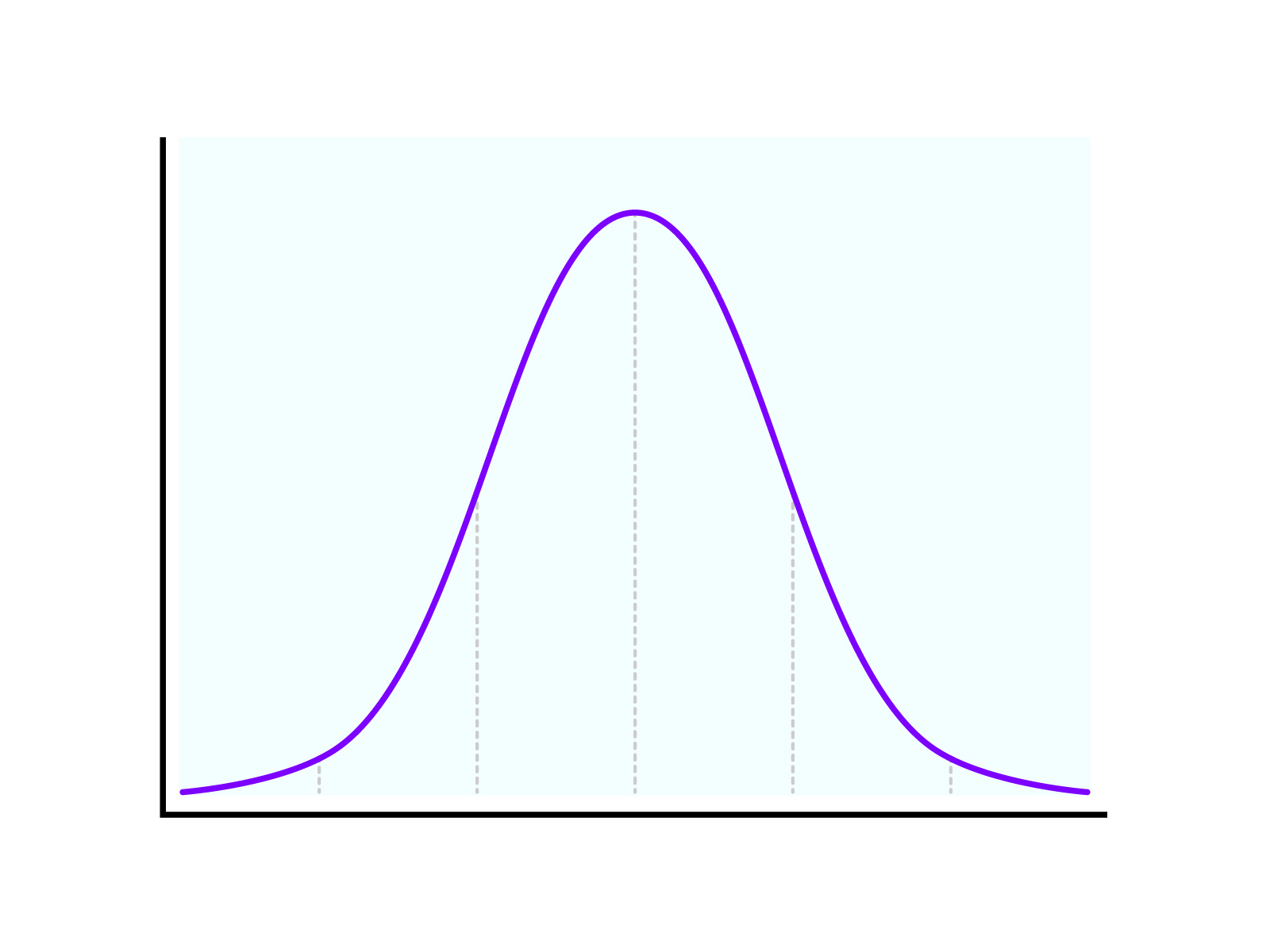
แต่เรื่องนี้ใช้ได้ก็ต่อเมื่อการกระจายข้อมูลเป็นการแจกจ่ายแบบปกติเท่านั้น

การแจกแจงปกติคือการแจกแจงที่ค่าเฉลี่ย มัธยฐาน และมัธยฐานร่วมกันและมีการกระจายแบบสมมาตรรอบแกน

ค่าเฉลี่ย = ผลรวมข้อมูล ÷ จำนวนข้อมูล

มัธยฐาน = ค่าที่เรียงจากน้อยไปหามากที่อยู่ตรงกลาง

มัธยฐานนิยม = ค่าที่พบมากที่สุดในข้อมูล

ตัวอย่างเช่นการแจกแจงความสูงของมนุษย์เป็นตัวอย่างที่ดี

ราคาค movement ไม่ได้แจกแจงแบบปกติ ดังนั้นข้ออ้างในโจทย์จึงผิดพลาด

การที่ราคาจะเกิน +2σ ไม่ได้บ่อยนัก

อย่างไรก็ตาม การที่ราคามาถึง +2σ และกลับมาที่ศูนย์กลางไม่เท่ากับการที่ราคาจะลดลงเสมอไป!

คุณเข้าใจข้อผิดพลาดทั่วไปเกี่ยวกับ Bollinger Band จากอินเทอร์เน็ตหรือหนังสือได้หรือยัง

ความน่าจะเป็นที่เกิน ±2σ น้อยกว่า 5% จึงไม่ใช่หลักฐานที่ราคาจะกลับตัว

การเคลื่อนไหวของราคามีแนวโน้มที่ไม่สมมาตร ดังนั้นแนวคิดที่ว่าราคาจะอยู่ภายในช่วง ±2σ จึงควรหยุดคิด

ถัดไป เราจะพูดถึงมุมมองสามประการในการมอง Bollinger Band