■ 1. ランダムウォークの世界は、基本“プラマイゼロ”

まず前提として、
「価格が完全にランダムに動く」世界では、長く待っても得もしないし損もしない という性質があります。これは、たとえばサイコロを何回振っても

平均したら出目が3.5になるのと同じです。上がるか下がるかは五分五分。だから平均したら±0。

これが“期待値0の世界”です。

■ 2. でも為替って、そんな単純じゃないんです

ここからが大事なところです。為替（ドル円）は、完全にランダムではありません。

むしろ、現実世界では――

行き過ぎれば戻りやすい

急激な変動には抑制がかかる

企業や投資家の行動が価格を引き戻す

政策も動く

輸出入のバランスも効く

こういった“現実の力”が働いています。

たとえばドル円が180円、200円と暴走すると輸出企業も輸入企業も動きますし、中央銀行も「さすがにやりすぎでは」と介入したりします。

反対に、ドル円が100円とか80円になれば、今度はアメリカ側が黙っていません。つまり、

為替は「行き過ぎたら戻る方向に働きやすい」という性質を持っているということです。

これが 平均回帰 です。

■ 3. 平均回帰があると、何が嬉しいの？

ランダムウォークだと、
利確ラインに触れずにずっと離れていくことが普通にあります。

でも平均回帰があると、話が変わります。

● OU過程というモデルで見ると…

平均に戻る力を数式化した OU（オーンスタイン＝ウーレンベック）過程では、

平均から離れたとき
→ 「戻る方向」に力が働く

平均に近づくと
→ 落ち着く

という動きをします。

これによって、

★ 利確ラインに“戻ってくる確率”が実際に高くなる

つまり、
「小さな利益なら、けっこう現実的に拾える」
ということです。ランダムウォークの場合はずっと待っていれば、値は戻ってくる一方で無限に離れてしまう可能性もあるから、期待値がゼロなのです。

■ 4. 「待てばたいていは利確しそう」という感覚は正しいの？

ここは誤解のないように、モデルで説明します。

平均回帰性があるほど、

平均に戻ろうとする力が強まる

だから利確ラインに触れやすくなる

のは確実にその通りです。

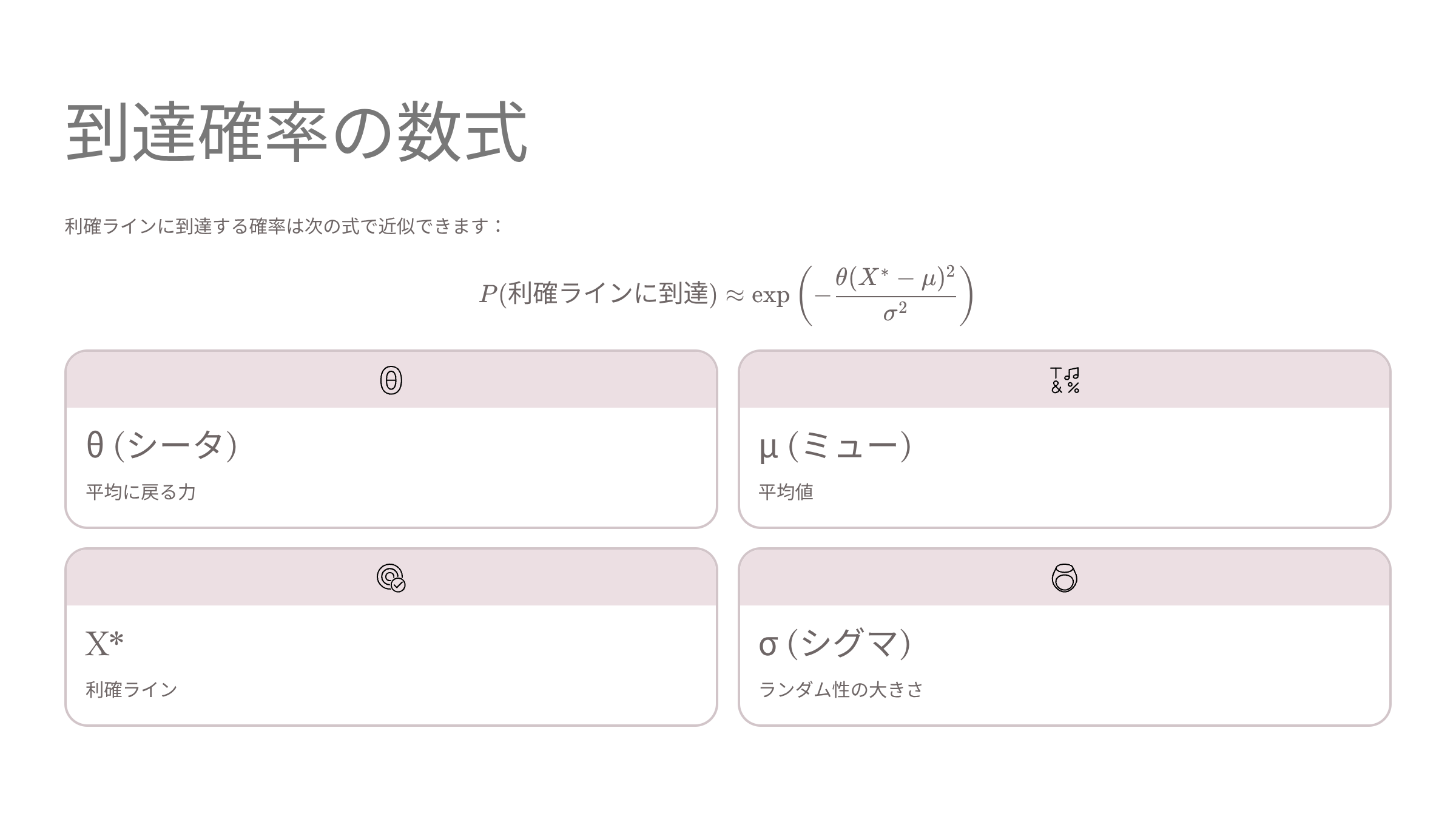
OU過程の hitting probability（到達確率）は次の式で近似できます：

$P (利確ラインに到達) \approx \exp (- \frac{θ (X^{*} - μ)^{2}}{σ^{2}})$

ここで、

$θ$ ：平均に戻る力

$μ$ ：平均値

$X^{*}$ ：利確ライン

$σ$ ：ランダム性の大きさ

となります。

■ 5. 実際、期待値はどうなるの？

この式から読み取れること：

戻る力 $θ$ が強いほど到達確率が上がる
利確ラインが平均に近いほど到達確率が上がる

ノイズ $σ$ が大きいと不安定になる

そして、ここが超大事。

★ 平均回帰があるなら、

★ ランダムウォークよりも“期待値は確実に上を向く”

利確幅を $a$ 、到達確率を上の式とすると、

$E = a \times P (利確)$

となります。

ランダムウォークでは $θ = 0$ なので、
上の式が 0に近い値になり、期待値も0に収まります。

ですが平均回帰があると、

★ $P (利確)$ が0より大きくなる

★ だから期待値も0より上を向く

という、ごく自然な話になります。

つまり、

平均回帰は、“小さな利確”の期待値を押し上げる本物の武器

です。

ここが今回の一番のポイントです。

■ 第4回まとめ

ランダムウォークでは何をやっても期待値は0です

実際の為替には“平均に戻る力”が働きます

これは企業・心理・政策など、現実の力から説明できます

モデル化すると OU 過程という形になります

平均回帰があると、利確ラインに触れる確率は高くなります

そのため期待値は0より上になる“余地が生まれます”

■ 次回予告（第5回）

次回は、
平均回帰の強さをいくつか変えながら、5000期間のシミュレーション

をグラフで視覚的に比較していきます。

第4回 ランダムウォークと為替の真実