[Trade] What are win rate, RR, and PF?

Question about Risk-Reward

“With a 40% win-rate technique, what minimum risk-reward is required to remain profitable? Also, explain why focusing on win-rate lowers the risk-reward.”

There are abundant books and content about win-rate, such as “high-win-rate methods!” and “trades with win-rate over 80%!”, but I have never heard of things like “methods with RR (risk-reward) of 2 or higher.”

I think most traders do not understand what is needed to win in trading.

Because they do not understand, they cannot engage in proper investment behavior, and they repeat the same mistakes year after year.

Win-rate is only one element of winning trades.

Answer

・Required risk-reward at 40% win-rate is 1.5 or higher
・When win-rate is prioritized, profit-taking comes earlier and stop-losses come later

Explanation

Win-rate = number of winning trades ÷ total number of trades
RR (risk-reward) = average profit ÷ average loss
PF (Profit Factor) = total profit ÷ total loss

Average profit = total profit from winning trades ÷ number of winning trades
Average loss = total loss from losing trades ÷ number of losing trades

Risk-reward is also called payoff ratio, and basically it expresses how many times the average profit per trade is relative to the average loss.

Let’s look at a concrete example.

In 10 trades, 4 wins with total profit of 400,000 and total loss of 300,000

Win-rate = 4 ÷ 10 = 0.4 (40%)
Average profit = 400,000 ÷ 4 = 100,000
Average loss = 300,000 ÷ 6 = 50,000
RR = 100,000 ÷ 50,000 = 2
PF = 400,000 ÷ 300,000 = 1.33

Profit for this trade is 400,000 − 300,000 = 100,000.

Expected value per trade is 100,000 ÷ 10 = 10,000.

PF = total profit ÷ total loss
= (average profit × win-rate) ÷ (average loss × loss-rate)
= (average profit ÷ average loss) × (win-rate ÷ loss-rate)
= RR × {win-rate ÷ (1 − win-rate)}

If PF exceeds 1, profit remains.

From this formula, you can determine the RR (risk-reward) needed to stay profitable at a given win-rate.

Let’s calculate for the given problem, win-rate 40%.

PF > 1

RR × {win-rate ÷ (1 − win-rate)} > 1

If you rearrange the equation,

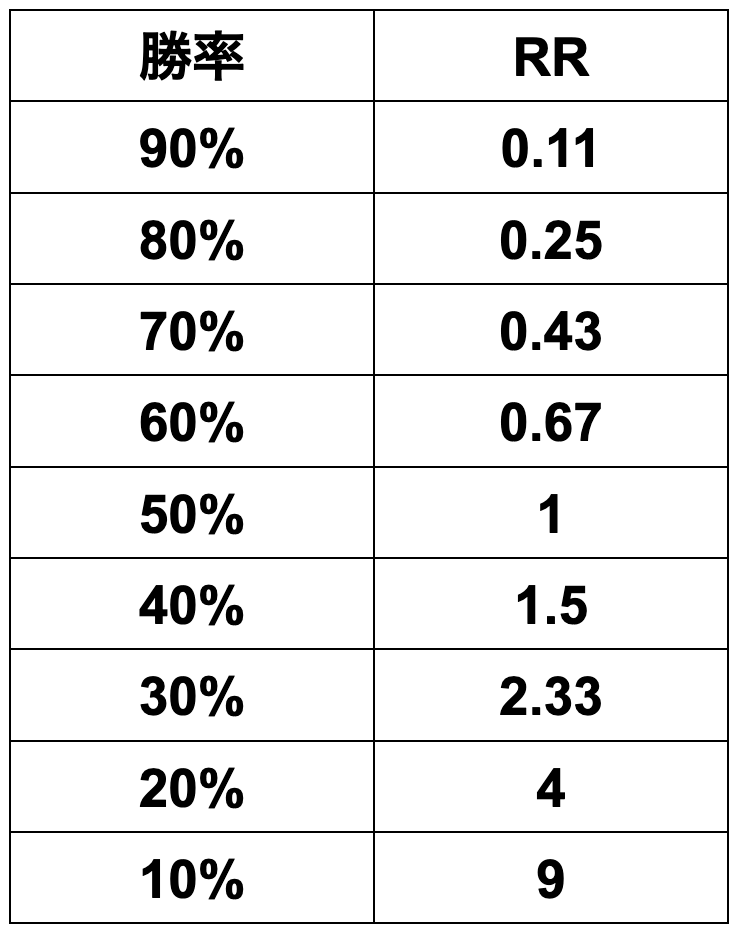
RR > (1 − win-rate) ÷ win-rate

Win-rate = 0.4, so

RR > (1 − 0.4) ÷ 0.4 = 1.5

This is the result.

Why win-rate-focused trading leads to a lower risk-reward is because

every win, whether it adds 10,000 or 1,000,000, is counted as a winning trade, so traders strive to close profit early to avoid unrealized losses.

On the other hand, if you are holding a losing position, you endure until it becomes profitable, causing the stop-loss to be delayed so that a winning trade can occur.

As the formula shows, PF is total profit ÷ total loss, so if total loss is 0, PF would be infinite.

That cannot happen, so eventually you will incur a large loss.

To win in trading, the rule is to maximize profit and minimize losses (losses small, profits large).

Be mindful of risk-reward in your trading.

Beating with counter-trend is difficult.

This is because win-rate and RR are in a trade-off relationship.

If RR is small and you want to raise win-rate,

you need to tighten the conditions for taking trades.

Thus, you will reduce the number of entries.

However, if each price move is small, you won’t make much money, so you would want to increase the number of entries.

If RR remains small while trying to raise win-rate, a contradiction arises.

It is possible to extend profits while reducing the number of entries.

Average profit × win-rate − average loss × loss-rate

This formula is called trading edge.

A method that yields profits with a reasonable number of trades has positive expectancy.

・Even with high win-rate, you can lose
・Even with low win-rate, you can win

By understanding the relationships among win-rate, RR, and PF, you can see that to win in trading, you need a positive trading edge.

Shift from win-rate-focused thinking to a focus on small losses and large gains, and switch your mindset to risk-reward!

Publicizing validation data for a trading rule that achieves small losses and large gains!

I will validate in your place: “Backtesting of trading rules for the past 20 years”